|
|
COLEGIO LA AMISTAD I.E.D GUÍA DE TRABAJO ESTRATEGIA
APRENDE EN CASA JORNADA TARDE |
|
Materia |
MATEMÁTICAS 401 – GUÍA 18 |
|
Docente |
HÉCTOR JULIO GUEVARA |
|
Ciclo/curso |
DOS/GRADO 401 |
|
Estudiante |
|
|
Fecha de desarrollo |
SEPTIEMBRE 7 Y 14 DE 2020 |
|
Competencias -Diferencia los
procesos y algoritmos para realizar operaciones básicas con fracciones
homogéneas y las simplifica. -Diferencia
los procesos o algoritmos para realizar operaciones básicas con fracciones
heterogéneas y las simplifica. |
|
|
Instrucciones
/procedimientos Esta guía es para
dos semanas, la actividad 1 se hace en la primera semana y la 2 en la
siguiente: 1. Lee toda la guía y asegúrate
de entender las explicaciones. 2. Realiza los ejercicios de
simplificación que se muestran en la guía. 3. Escribe como se suman y restan
fracciones homogéneas, con los ejemplos. 4. Escribe cómo se suman y restan
fracciones heterogéneas, con ejemplos. 5. Explica cómo se multiplican
fracciones y escribe dos ejemplos. 6. Explica cómo se dividen
fracciones y escribe dos ejemplos. 7. Realiza en tu cuaderno los
ejercicios de aplicación que están al final de la guía. 8. Envía tus actividades al
correo profehectorj2020@gmail.com |
|
|
Contenidos. 1. SIMPLIFICACIÓN DE
FRACCIONES: Simplificar significa hacer más
simple un número fraccionario y es muy útil para representar fracciones. Para
simplificar se debe dividir el numerador y el
denominador de una fracción por el mismo número para
que no se altere, de la siguiente forma: OPERACIONES CON FRACCIONES
SUMA, RESTA, MULTIPLICACIÓN Y DIVISIÓN. Antes de realizar
cualquier operación con números fraccionarios es necesario recordar que hay
fracciones HOMOGÉNEAS, que tienen el mismo denominador y fracciones
HETEROGÉNEAS que tienen diferente denominador. El procedimiento será
diferente en cada caso. SUMA Y RESTA DE
FRACCIONES HOMOGÉNEAS: En este caso se
suman o se restan los numeradores y se deja el mismo denominador. Si se puede
se debe simplificar.
SUMA Y RESTA DE
FRACCIONES HETEROGÉNEAS: Cuando el
denominador de las fracciones es diferente se debe reducir a un común
denominador de la siguiente forma: 1.Multiplicar los denominadores para obtener
un denominador común. (3x4) 2.Multiplicar el numerador del primero por
el denominador del segundo, es decir multiplicar en cruz (2x4). Luego el
numerador del segundo por el denominador del primero (3x3). 3.Se suman o restan los numeradores y se
coloca el denominador común (8+9/12). 4.Finalmente se simplifican o divide el
numerador y denominador por el mismo número hasta el número más pequeño.
(para el ejemplo no se puede ya que 17 es un número primo). 2. MULTIPLICACIÓN DE
FRACCIONES: En este caso no se
diferencia entre homogéneas y heterogéneas, solo se deben multiplicar los numeradores
y luego los denominadores y si es necesario se debe simplificar al final: DIVISIÓN DE
FRACCIONES: Para esta operación
tampoco se tiene diferencia entre fracciones homogéneas y heterogéneas, el
proceso es sencillo, basta con multiplicar en cruz, es decir el numerador del
primero por el denominador del segundo y luego el denominador del primero por
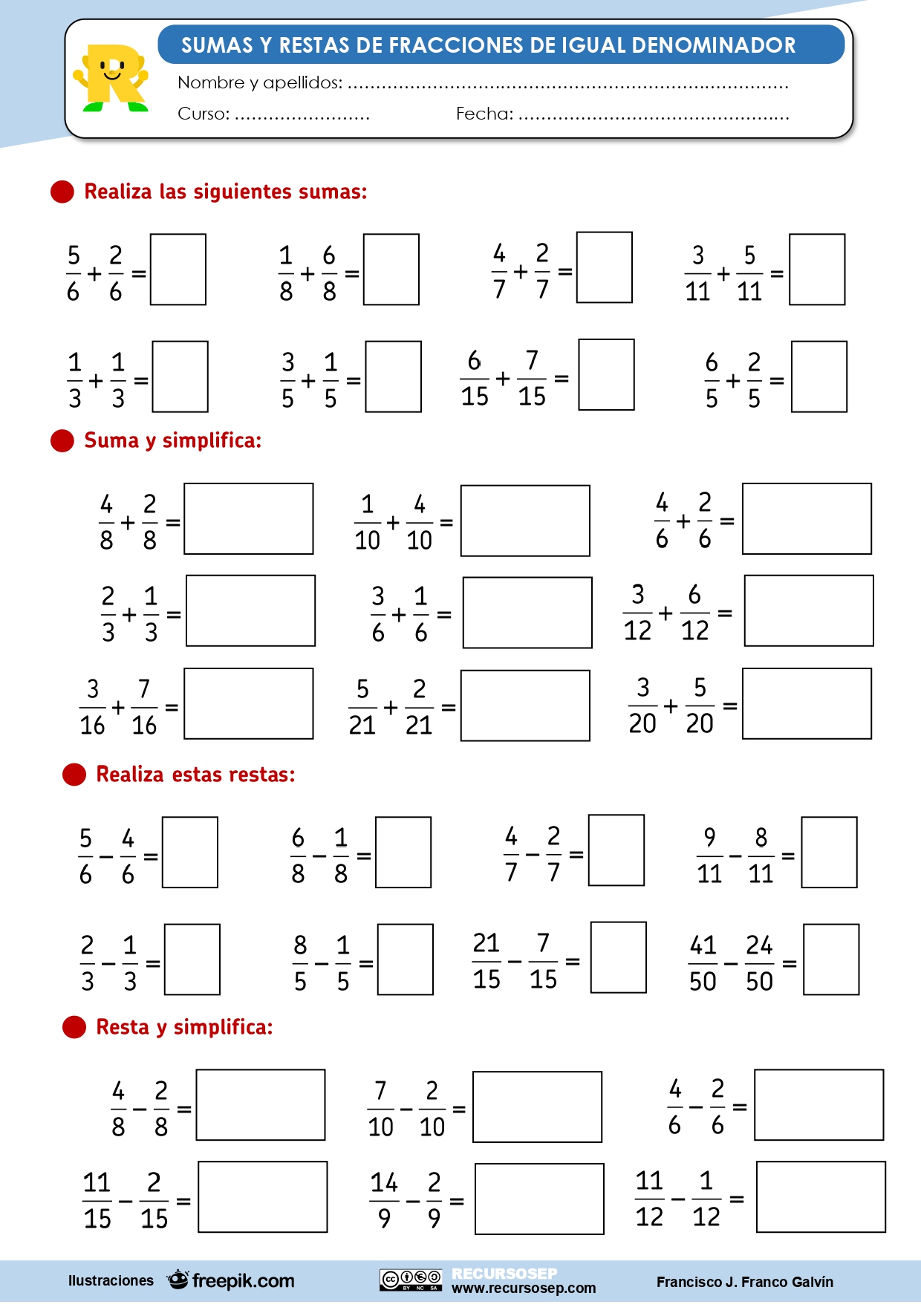
el numerador del segundo así: Ahora realiza los
siguientes ejercicios con fracciones homogéneas y heterogéneas: |
|
|
Links Video de apoyo. https://youtu.be/DbVigRe7lnU |
|
|
Bibliografía Valero, A. (2005).
Guía escolar 4. Bogotá. Santillana Colombia mía. Ardila, V. H. (2000).
Olimpiadas matemáticas 4. Bogotá. Editorial voluntad |
|






No hay comentarios:
Publicar un comentario